In the last post I talked about some of the basics of structural biology. I'm focusing on these annoying loops that form part of the antibody - the bits that do the work. My theory is maybe neural networks can do a better job than other methods thus far. But how do we even begin to approach this problem? How can we go from a list of amino acids to a full 3D structure?
Amino acids have an amine and carboxyl group, with what is known as a sidechain that hangs off the side. I'm no chemist, so I'm sure someone out there will tell me what these words mean. But for our purposes, what we need to know is the amine and carboxyl groups form a backbone - a (polypeptide) chain if you will. It is this chain that we want to chase. For now, we don't actually need to know the sidechain details.
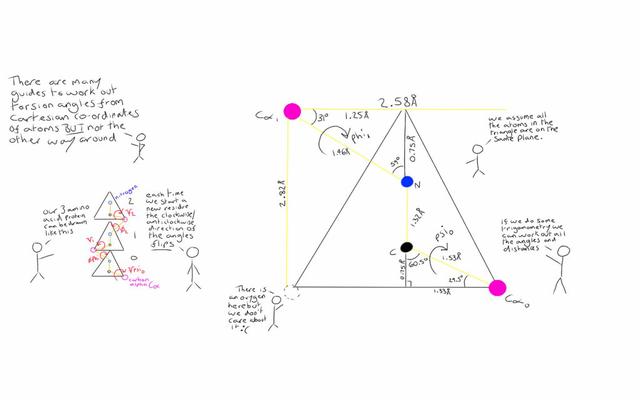
Furthermore, we can represent this backbone using three dihedral angles, known as phi, psi and omega. Looking at the backbone we can count along each acid (known as a residue) and read off the atoms. If we start from the 5 prime end, we get: nitrogen, carbon, carbon, nitrogen, carbon... etc

The first carbon atom we come across is known as the Alpha Carbon (Ca). The second is the Carboxyl Carbon (C). So for each residue, we have N-Ca-C, N-Ca-C, and repeat. If we know the distances and angles between these atoms we can calculate these dihedral angles. From these angles we can recreate the structure again if we need to.
A dihedral angle is essentially the angle between two planes that intersect. We take 4 atoms in our structure, find the two planes then the angle between them. Phi is the twist around the Alpha Carbon and the Nitrogen, with Psi being the twist around the Carboxyl Carbon and the Alpha Carbon.
Omega is a bit of a special case. It is the twist around the Nitrogen and the Carboxyl Carbon but it very rarely changes from around 180 degrees. It hovers roughly +/- 15 degrees from this, except in special cases. As with so many things in biology, there is always a special case!
There has been some interesting work of late in creating 3D objects with neural networks. As far as I can tell, there are two main ways to create 3D structures; combining existing ones and discretising the space. There are a few workshops and conferences such as CVPR, 3DDL at NIPS, some github repositories like Synthesize3,3D pose estimation and Deep Lung. So far, the field seems to be fairly new, with most of the code being on the bleeding edge.
Fortunately, we don't have to do any of that. Angles can be represented as two numbers, the sin and cosine of the angle in question. Both of these functions range from -1 to 1 and can therefore fit nicely in to the classic model of a neuron in our network. If we use tanh as oppose to something like a ReLU, we can cover this range quite comfortably (we can ignore the slight non-linear problem here for now - we are hacking this somewhat!).
So how do we go from angles back to a structure we can look at in order to do a comparison? One could do an awful lot of trig, but there is a more elegant algorithm called NeRF (and sn-NeRF). Annoyingly, the paper is behind the Wiley paywall, but the general gist of the algorithm is to start with 3 atoms, and place the next atom based on the positions of the previous three.
NeRF has two steps. Firstly, the atom is placed using the known bond angles, distances and the previous positions using a little trigonometry with the bond and torsion angles. The last step creates a matrix that rotates the atom into the correct reference plane.
The paper misses out two vital issues! One thing the paper does not go into is the fact that one should start from a Nitrogen at the 5 prime end! I've been trying to go from the 3 prime end, and it didn't really work so well. I suspect this is one of these cases where the knowledge is just assumed in that domain. Secondly, there is a cheeky minus sign in the second section X value.
I had a little help from James Phillips at the London Biohackspace who took at look at my code, and noticed the 5 prime issue! Always good if you can get another person to look over your code when you are stuck.
Here is the NeRF algorithm in full, in Python for these who might want it.
import numpy as np
import math, itertools
class NeRF(object):
def __init__(self):
# TODO - PROLINE has different lengths which we should take into account
# TODO - A_TO_C angle differs by +/- 5 degrees
#bond_lengths = { "N_TO_A" : 1.4615, "PRO_N_TO_A" : 1.353, "A_TO_C" : 1.53, "C_TO_N" : 1.325 }
self.bond_lengths = { "N_TO_A" : 1.4615, "A_TO_C" : 1.53, "C_TO_N" : 1.325 }
self.bond_angles = { "A_TO_C" : math.radians(109), "C_TO_N" : math.radians(115), "N_TO_A" : math.radians(121) }
self.bond_order = ["C_TO_N", "N_TO_A", "A_TO_C"]
def _next_data(self, key):
''' Loop over our bond_angles and bond_lengths '''
ff = itertools.cycle(self.bond_order)
for item in ff:
if item == key:
next_key = next(ff)
break
return (self.bond_angles[next_key], self.bond_lengths[next_key], next_key)
def _place_atom(self, atom_a, atom_b, atom_c, bond_angle, torsion_angle, bond_length) :
''' Given the three previous atoms, the required angles and the bond
lengths, place the next atom. Angles are in radians, lengths in angstroms.'''
# TODO - convert to sn-NeRF
ab = np.subtract(atom_b, atom_a)
bc = np.subtract(atom_c, atom_b)
bcn = bc / np.linalg.norm(bc)
R = bond_length
# numpy is row major
d = np.array([-R * math.cos(bond_angle),
R * math.cos(torsion_angle) * math.sin(bond_angle),
R * math.sin(torsion_angle) * math.sin(bond_angle)])
n = np.cross(ab,bcn)
n = n / np.linalg.norm(n)
nbc = np.cross(n,bcn)
m = np.array([
[bcn[0],nbc[0],n[0]],
[bcn[1],nbc[1],n[1]],
[bcn[2],nbc[2],n[2]]])
d = m.dot(d)
d = d + atom_c
return d
def compute_positions(self, torsions):
''' Call this function with a set of torsions (including omega) in degrees.'''
atoms = [[0, -1.355, 0], [0, 0, 0], [1.4466, 0.4981, 0]]
torsions = list(map(math.radians, torsions))
key = "C_TO_N"
angle = self.bond_angles[key]
length = self.bond_lengths[key]
for torsion in torsions:
atoms.append(self._place_atom(atoms[-3], atoms[-2], atoms[-1], angle, torsion, length))
(angle, length, key) = self._next_data(key)
return atoms
if __name__ == "__main__":
nerf = NeRF()
print ("3NH7_1 - using real omega")
torsions = [ 142.951668191667, 173.2,
-147.449854444109, 137.593755455898, -176.98,
-110.137784727015, 138.084240732612, 162.28,
-101.068226849313, -96.1690297398444, 167.88,
-78.7796836206707, -44.3733790929788, 175.88,
-136.836113196726, 164.182984866024, -172.22,
-63.909882696529, 143.817250526837, 168.89,
-144.50345668635, 158.70503596547, 175.87,
-96.842536650294, 103.724939588454, -172.34,
-85.7345901579845, -18.1379473766538, -172.98,
-150.084356709565]
atoms0 = nerf.compute_positions(torsions)
print(len(atoms0))
for atom in atoms0:
print(atom)
NeRF isn't perfect; it makes some assumptions that don't always hold up. The distances given at the top do vary, though they have been verified by a few experiments. Adding in this variation might be something I implement in the future, but for now, NeRF recreates the majority of structures quite well.
With a representation of the chain as a series of angles, we can build several different kinds of networks that, when given a series of amino acids, produce a set of numbers ranging from -1 to 1. Recombining the sin and cosine, converting to degrees and applying NeRF, we get a structure that is very close to the original.
In the next blog post, I'll look at the different kinds of networks, which work best and what pitfalls we need to avoid.
